 Florenci Pla – Director del Centre d’Estudis Empresarials i Tecnològics de la Universitat d’Andorra.
Florenci Pla – Director del Centre d’Estudis Empresarials i Tecnològics de la Universitat d’Andorra.
La velocitat generalment s’associa a la rapidesa del moviment. Si un cos es mou (canvia de posició) molt ràpid (amb poc temps) direm que la seva velocitat és molt alta i si un cos no és mou direm que la velocitat és nul·la (està parat).
Així doncs abans d’entrar a parlar de velocitat caldrà que tinguem molt clars els conceptes moviment i repòs. Un cos està en moviment si canvia de posició en l’espai i un cos està en repòs si roman en el mateix lloc. Fins aquí, cap problema no?.
Ara bé, aquestes definicions comporten que prèviament s’hagi fixat la posició del cos respecte a un sistema de referència. I és aquí on venen els problemes.
Per explicar el sistema de referència ens basarem en un exemple concret. Imaginem-nos que agafem l’AVE a Lleida en sentit a Madrid (alguns dirien, de forma incorrecta, en direcció a Madrid, ja que sovint i de forma col·loquial es confon sentit i direcció), seiem al lloc assignat, arranca el tren i al cap de pocs minuts ja anem a 250 km/h. La pregunta és, en aquest moment estem en repòs o en moviment?
Per un observador que estigui dins del vagó, estem en repòs ja que la nostra posició no canvia (a no ser que anem al bar a prendre alguna cosa, romandrem asseguts al mateix seient). En canvi un pagès que treballa la terra (la terra de la Terra, més endavant veureu perquè faig aquest aclariment) al costat de la via veu que ens movem a 250 km/h. Així doncs, estem en moviment respecte a un observador que estigui fora del tren (el pagès) i estem parats per un observador que estigui dins del tren i en conseqüència podem dir estem parats o en moviment en funció del punt de referència. En aquest cas, estem en repòs per a qualsevol observador, quiet, del vagó i estem en moviment (ens movem a 250 km/h) per a un observador que es trobi, quiet, a l’exterior del tren.
Continuem el viatge. Suposem ara que l’AVE s’atura a l’estació de Saragossa i que continuem asseguts al nostre seient. Estarem en repòs o en moviment? En aquest cas estarem en repòs tant per a un observador del vagó com per a un observador extern al vagó (un que estigui de l’andana). Així doncs, estàs en repòs en relació al vagó i en relació a la Terra. Ara sembla que no hi ha dubte, estem en repòs es miri com es miri.
Doncs no, ja que la Terra dóna voltes sobre si mateixa (moviment de rotació) a una velocitat, a l’Equador, d’aproximadament 1.667km/h. Així doncs, per a un observador, quiet, situat a l’exterior de l’atmosfera terrestre estaríem en moviment. Per aquest observador ens mouríem donant voltes a més de 1.500 km/h ja que aquest observador no pot diferenciar si el que es mou és la Terra o és l’AVE.
I encara més. La Terra no només gira sobre el seu eix a una velocitat d’aproximadament 1.667km/h sinó es trasllada al voltant del Sol (moviment de translació) a una velocitat mitjana de 35 km/s i també ens estem movent amb aquest velocitat. És a dir, si parats a l’estació de Saragossa poguéssim parlar amb un observador, que es trobi al Sol, i li diguéssim “Estic parat a l’estació de Saragossa i …” , ell ens diria “Parat? Si veig que dones voltes a la Terra una velocitat de més de 1.500km/h a la vegada que et desplaces a una velocitat de 35 km/s ,,,” i així podríeu estar discutint de moviment i repòs durant una bona estona. Ah! I els dos tenim raó ja que no tenim el mateix punt de referència.
Ja ho veieu encara que ens sembli que estem immòbils a l’estació de l’AVE de Saragossa, estem realitzant un viatge pel Sistema solar a més de 3.000.000 km/dia, però resulta que el Sol també es mou dins de la Galàxia i aquesta també es mou i …..
Així doncs, no podem saber si estem en moviment o en repòs d’una manera absoluta ja que necessitaríem un punt fix. Però no hi ha cap punt fix a l’Univers, sinó que tot es mou: el vagó, la Terra, el Sol, les estrelles, les galàxies etc. És en aquest sentit que no es pot parlar de moviment o repòs absoluts, només podem fer-ho de forma relativa respecte a un punt que considerarem fix (en ciència es fa molt de fer consideracions).
Per tant, com que no hi ha observadors privilegiats (fixos) hem de definir el moviment i el repòs respecte a sistemes de referència que considerem fixos, encara que hem de ser conscients que no ho són.
Una vegada clarificat que vol dir moviment entrem en el concepte de velocitat. Podríem dir que la velocitat mesura com de ràpid canviem de posició. De tots és coneguda la fórmula.
Velocitat = espai / temps
Així doncs, si el vehicle A triga menys temps que el vehicle B en fer el mateix recorregut direm que A va més ràpid que B. Això ens indica que les magnituds temps i velocitat són inversament proporcional (si una augmenta l’altra disminueix amb la mateixa proporció).
Errors comuns en el càlcul de velocitats
Un error molt comú és confondre la velocitat mitjana amb la mitjana de les velocitats. Per exemple si anem d’A a B a 100 km/h i tornem (de B a A) a 50 km/h, quina ha estat la velocitat mitjana de tot el trajecte d’anada i tornada?
El més habitual és que un pensi que és la mitjana de velocitats,
 i es quedi tant ample.
i es quedi tant ample.
Comprovem-ho amb un cas pràctic per fer-ho més fàcil. Imaginem que la distància A-B és de 100 km. Llavors tenim que a l’anada triga 1 h i a la tornada 2h. Això vol dir que ha fet 200 km (100 km d’anada i 100 km de tornada) en 3h (1h d’anada i 2 h de tornada) amb la qual cosa la velocitat mitjana ha estat de 200 km/ 3h = 66,67 km/h (bastant per sota dels 75 km/h).
Aquest raonament (velocitat mitjana = mitjana de velocitats) només el podem fer quan anem el mateix temps a velocitats diferents. Per exemple si durant 1h anem a 100 km/h i durant una altra hora anem a 50 km/h, sí que la velocitat mitjana és de 75 km/h, ja que hem recorregut 150 km (100 km la primera hora i 50 km la segona) en dues hores, amb la qual cosa la velocitat mitjana ha estat de 150 km/2h = 75 km/h
Ara que ja ho tenim una mica més clar, intentem resoldre la següent situació: “Un ciclista puja un port de muntanya amb una velocitat mitjana de 10 km/h. Quina haurà de ser la velocitat de baixada perquè la velocitat mitjana total (pujada i baixada) sigui de 20 km/h?”
Possiblement alguns de vosaltres per mandra d’agafar un paper i llapis i pensar-ho un mica direu: “Si ha pujat a 10 km/h i vol obtenir una mitjana de 20 km/h només caldrà que baixi a 30 km/h ja que:
\(20=\frac{10+30}{2}\)
Doncs no. Aquesta no és la solució, seria massa fàcil. I encara us diria més, per molt ràpid que baixi, mai podrà aconseguir fer una mitjana de 20 km/h. Sorprenent, no?
Aquest afirmació tant rotunda (i sorprenent) requereix una explicació. Imaginem que el port de muntanya té “X” km.
Raonament (1)
Si pugem el port a 10 km/h trigarem X/10 hores en arribar a dalt.
El temps que trigarem en baixar el port serà X/v. Essent v la velocitat de baixada.
Si ha de fer una mitjana de 20 km/h, entre pujar i baixar, tindrem que:

D’aquí deduïm que és impossible fer una mitjana de 20 km/h entre pujar i baixar si la velocitat mitjana de pujada ha estat de 10 km/h.
Raonament (2)
Si el pugem a 10 km/h trigarem X/10 hores en arribar a dalt.
Si féssim una mitjana de 20 km/h entre pujar i baixar voldria dir que el temps emprat entre la pujada i baixada seria de $$\frac{2x}{20}\$$=$$\frac{x}{10}\$$, que com podem veure és igual al de la pujada. D’aquí deduïm que el temps de baixada hauria de ser zero i això és impossible.
Raonament (3)
Imaginem que el ciclista triga t hores en pujar-lo i t’ en baixar-lo. Com que la velocitat mitjana de pujada és de 10 km/h tindrem que X= 10·t.
Per calcular la velocitat mitjana total, com que pujada+baixada=2·X tindrem que:
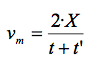
I com que volem que Vm=20 km/h tindrem que :
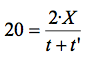
o sigui:
![]()
Ara bé, abans hem vist que X=10·t amb la qual cosa 2·X=20·t que substituint a l’equació $$2x = 20t+20t’$$, tindrem que $$2x = 2x + 20t’$$. És a dir, 20·t’=0 i en conseqüència t’=0. Això vol dir que per fer una mitjana total de 20 km/h hauria de fer el descens del port amb un temps zero, i això és impossible per molt ràpid que sigui el descens.
Per a quines altres velocitats mitjanes trobarem aquesta impossibilitat? Seguint el raonament anterior ens adonem que aquesta impossibilitat és dóna sempre que vulguem obtenir una velocitat mitjana total superior o igual al doble de la velocitat aconseguida a l’anada. En el nostre cas concret podem aconseguir una velocitat mitjana propera 20 km/h (sempre i quan baixem com un llamp), però mai de 20 km/h. Curiós, no?
Velocitat màxima i mínima
Possiblement ningú dubtaria que si anem cada vegada més a poc a poc arribarà un moment ens aturarem (velocitat zero) i podríem dir que aquesta és la velocitat mínima. Quan estem parats ja no es pot anar més a poc a poc.
Ara bé, i la velocitat màxima? Un podria pensar que no hi ha límit, ja que com més energia comuniquem a un cos més gran és la seva velocitat i no sembla que hi hagi cap raó (o si) que impedeixi acostar-nos a la velocitat de la llum i fins tort a superar-la. Doncs no és així.
La màxima velocitat que es podria agafar són els quasi 300.000 km/s que és la velocitat de la llum al buit. Això ho explica la teoria de la relativitat d’Einstein que plateja que la massa d’un cos pot considerar-se una forma d’energia (E=m·c2) però no entrarem en la seva demostració.
Com podeu veure el concepte i càlcul de velocitats és bastant senzill, però sovint existeixen moltes idees errònies al respecte.